参考自LeetCode上Explore模块的Queue & Stack,作为笔记记录。
Overview 综述
主要了解两种不同的元素处理顺序:先入先出(FIFO)和后入先出(LIFO);以及两个相应的线性数据结构:队列(Queue)和栈(Stack)。
主要内容:
- 了解 FIFO 和 LIFO 处理顺序的原理;
- 实现这两个数据结构;
- 熟悉内置的队列和栈结构;
- 解决基本的队列相关问题,尤其是
BFS; - 解决基本的栈相关问题;
- 理解当你使用
DFS和其他递归算法来解决问题时,系统栈是如何帮助你的。
Queue: First-in-first-out Data Structure 队列:先入先出的数据结构
先入先出的数据结构
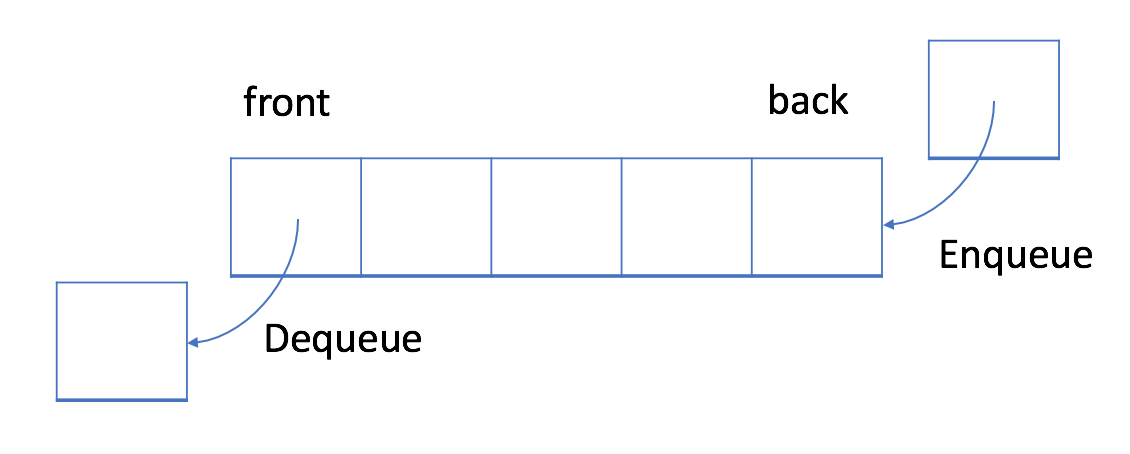
FIFO数据结构:首先处理添加到队列中的第一个元素。
队列是典型的FIFO数据结构,插入删除操作被称为入队出队,新元素始终添加在队列末尾,只能移除第一个元素。
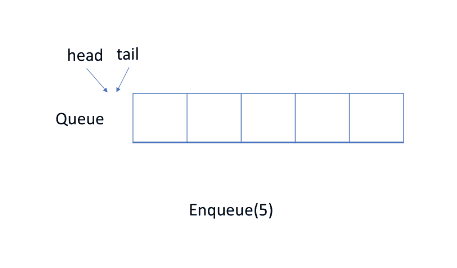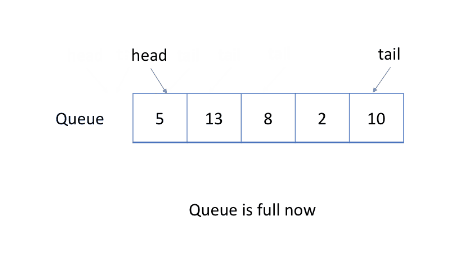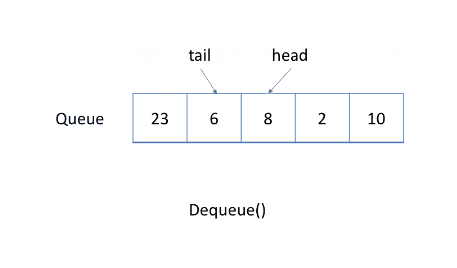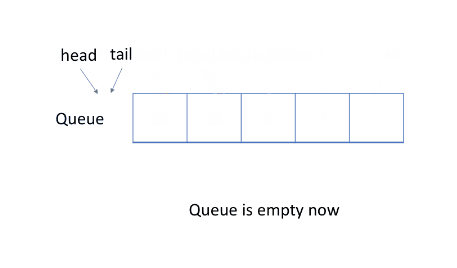
循环队列
简单的使用动态数组和指向队列头部的索引来实现队列,会导致空间的浪费。
更有效的方法是使用循环队列,即使用固定大小的数组和两个指针来指示起始位置和结束位置,目的是重用被浪费的存储空间。
示例如图:
练习:设计循环队列
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
MyCircularQueue(k): 构造器,设置队列长度为 k 。Front: 从队首获取元素。如果队列为空,返回 -1 。Rear: 获取队尾元素。如果队列为空,返回 -1 。enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。isEmpty(): 检查循环队列是否为空。isFull(): 检查循环队列是否已满。
示例:
1 | MyCircularQueue circularQueue = new MycircularQueue(3); // 设置长度为 3 |
提示:
- 所有的值都在 0 至 1000 的范围内;
- 操作数将在 1 至 1000 的范围内;
- 请不要使用内置的队列库。
解答:设计循环队列
使用一个数组和两个指针(tail和head)表示队列的结束和起始位置。
代码如下:
1 | class MyCircularQueue { |
队列:用法
大多数语言都提供内置的队列库,无需重复造轮子。
以C++内置队列库使用为例:
1 |
|
当想要按顺序处理元素时,使用队列可能是一个很好的选择。
练习:Moving Average from Data Stream
【LeetCode】346
Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
For example,
1 | MovingAverage m = new MovingAverage(3); |
计算滑动窗口中数字的平均数。
用队列模拟窗口,队列长度为窗口大小,超过时则将首元素移出队列,返回当前队列的平均数即可。
代码如下:
1 | class MovingAverage { |
Queue and BFS 队列和广度优先搜索
广度优先搜索(BFS)是一种遍历或搜索数据结构的算法。
可以用BFS执行树的层序遍历,可以遍历图并找到从起始节点到目标节点的路径(特别是最短路径)。
队列和BFS
BFS的一个常见应用是找从根节点到目标节点的最短路径。
下图展示用BFS找出节点A到目标节点G的最短路径。
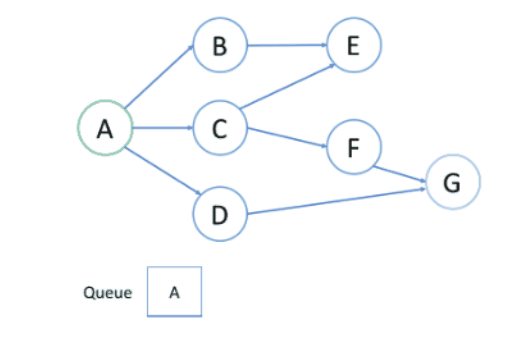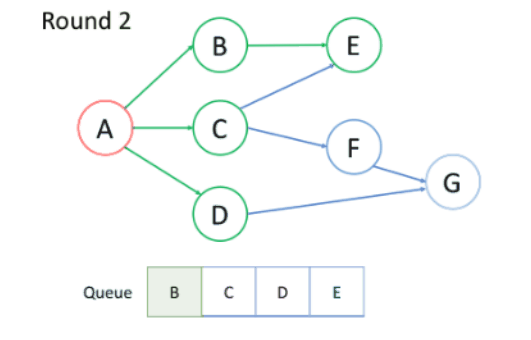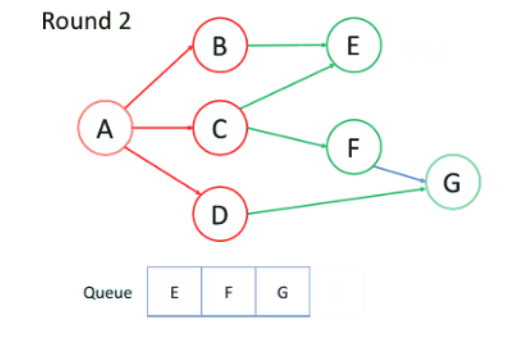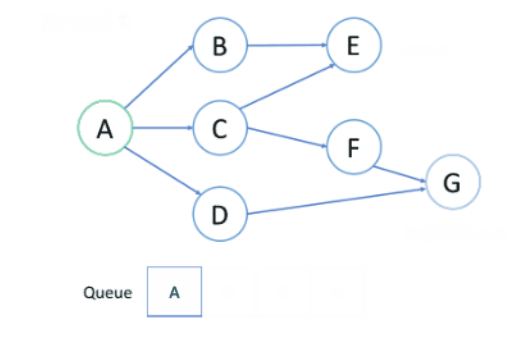
上述过程中:
节点处理顺序:越是接近根节点的节点将越早被遍历,所以第一次找到目标节点时,即为最短路径。
入队出队顺序:首先根节点入队,之后每轮处理已经在队列中的点,并将所有邻居入队,新加入的节点将在下轮处理,节点处理顺序与入队的顺序相同,即FIFO,所以BFS过程中可以使用队列处理问题。
广度优先搜索——模板
使用BFS的两个主要场景:遍历或找出最短路径。
BFS也可以用于更抽象的场景中,在特定问题中执行BFS之前确定节点和边缘非常重要。通常,节点是实际节点或状态,而边缘是实际边缘或可能的转换。
伪代码模板(Java):
1 | /** |
如果需要确保不会访问一个节点两次,可以在上述代码中加入一个set来记录访问过的节点,如下所示:
1 | /** |
练习:walls and gates
【LeetCode】286
You are given a $m*n$ 2D grid initialized with these three possible values.
给定一个的用如下三个可能值初始化的$m*n$的2D网格。
-1- A wall or an obstacle. 墙壁或障碍物。0- A gate. 门。INF- Infinity means an empty room. We use the value $2^{31}-1=2147483647$ to representINFas you may assume that the distance to a gate is less than2147483647. Infinity是一个空房间,使用值$2^{31}-1=2147483647$来表示INF,可以假设到门的距离小于2147483647。
Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF. 在每个代表空房间的网格中填充其距离最进门的距离,如果不可能到达门,则填充INF。
For example, given the 2D grid:
1 | INF -1 0 INF |
After running your function, the 2D grid should be:
1 | 3 -1 0 1 |
代码如下:
要注意节点的判断;
1 | class Solution { |
练习:岛屿的个数
给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例 1:
1 | 输入: |
示例 2:
1 | 输入: |
解题思路
采用广度优先遍历的方法还是很容易解决这个问题的,我们尝试遍历所有的点,如果一个点是陆地且从未遍历过,则认为发现了新岛屿,在发现了新岛屿后使用广度优先的方式扩展该岛屿以防止重复计数.
代码如下(含完整测试代码):
1 |
|
练习:打开转盘锁
【LeetCode】752
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出最小的旋转次数,如果无论如何不能解锁,返回 -1。
示例 1:
1 | 输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202" |
示例 2:
1 | 输入: deadends = ["8888"], target = "0009" |
示例 3:
1 | 输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888" |
示例 4:
1 | 输入: deadends = ["0000"], target = "8888" |
提示:
- 死亡列表
deadends的长度范围为[1, 500]。 - 目标数字
target不会在deadends之中。 - 每个
deadends和target中的字符串的数字会在 10,000 个可能的情况'0000'到'9999'中产生。
解题思路
找最短路径问题,考虑用BFS,将问题建图。
每个字符串对应一个状态,可以转换到相邻的8个状态(每位加1减1,共4位),从“0000”开始进行BFS,最后得到总步骤数。
类似用BFS遍历图,找最短路径,所以第一次到达目标节点时的路径一定是最短路径(之一)。
- 注意向相邻节点转换时的操作,“0”->“9”,“9”->“0”,加1,减1;
- 用unordered_set存储访问标记和死亡节点,节省查找过程的时间消耗;
- 首先对deadends进行去重,看讨论区有说会有重复的情况;
- BFS:从头结点”0000”开始,遍历所有子节点,初次访问且不在deadends中的则入队;已访问过或在deadends中的则跳过;遍历到下一层时,层数step加1,且更新size为下一层的节点数量;
- 每访问一个节点,先判断是否target,若是则返回当前的step;如果队列已空但仍未返回,则说明无路可通。
代码如下:
1 | class Solution { |
练习:完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
1 | 输入: n = 12 |
示例 2:
1 | 输入: n = 13 |
解题思路
参考网上的思路,转换为最短路径问题。
从$0$到$n$共有$n+1$个节点,如果从$i , i\in[0,n]$到$j , j\in[0,n]$相差一个完全平方数,就可以将两个节点连接起来,这样所有的点就转化成无向图,问题转化为求从$0$到$n$的最短路径。
如图所示:
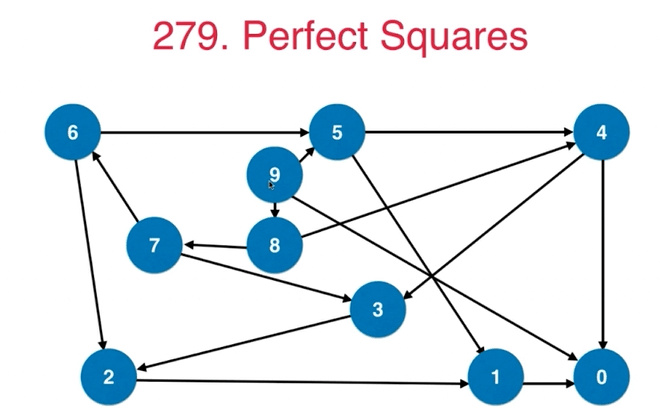
无权最短路径问题,可以采用BFS求解。
也就是说,先遍历从$[1,ii],ii\leq n$,每一步将$n$缩为$n-i*i$,广度优先搜索,直至找到第一条将$n$缩为$0$的路径,即为最短路径。如下所示:
1 | //将num不断用完全平方数代表,直至其成为0,其中1是完全平方数所以总会有解 |
完整代码如下:
1 | class Solution { |
Stack: Last-in-first-out Data Structure 栈:后入先出的数据结构
后入先出的数据结构
LIFO数据结构:首先处理添加到队列中的最新元素。
栈是典型的LIFO数据结构,插入删除操作称为入栈(push)出栈(pop),新元素始终添加在堆栈的末尾,只能移除堆栈中的最后一个元素。
动态数组可用来实现堆栈结构。
栈:用法
大部分语言都有内置的栈库,无需重复造轮子。
以C++内置库的使用为例:
1 |
|
当想要首先处理最后一个元素时,栈将是最合适的数据结构。
练习:最小栈
设计一个支持 push,pop,top 操作,并能在常数时间内检索到最小元素的栈。
- push(x) — 将元素 x 推入栈中。
- pop() — 删除栈顶的元素。
- top() — 获取栈顶元素。
- getMin() — 检索栈中的最小元素。
示例:
1 | MinStack minStack = new MinStack(); |
解题思路
方法一,可以用两个栈,一个是题意要求的栈,另一个用来存储每次push后的当前最小值,push或pop时,同时修改两个栈的内容,存最小值的栈的top即为当前全栈最小值。
方法二,只用一个栈,再用一个额外的变量存储当前最小值。每次push时,如果要入栈的值比当前最小值小,则将当前最小值和要入栈的值同时入栈(注意先后顺序),每次pop时,要比较即将出栈的值和当前最小值是否相同,如果相同,则意味着当前最小值要更改为下一个栈顶元素(当前最小值和更新的最小值在栈内相邻)。
代码如下:
1 | class MinStack { |
练习:有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
示例 1:
1 | 输入: "()" |
示例 2:
1 | 输入: "()[]{}" |
示例 3:
1 | 输入: "(]" |
示例 4:
1 | 输入: "([)]" |
示例 5:
1 | 输入: "{[]}" |
解题思路
用栈结构,遍历字符串,如果是左括号就入栈,如果是右括号就看是否和栈顶元素是一对,如果是则出栈并继续,如果不是一对则返回false,如果遍历结束时栈为空则返回true,如果遍历结束时栈不为空则返回false(如”((“的情况)。
需要判断一些特殊情况,如s长度为0则直接返回true,如果s长度为奇数则直接返回false,同时top时要先确认栈非空。
代码如下:
1 | class Solution { |
练习:每日温度
根据每日 气温 列表,请重新生成一个列表,对应位置的输入是你需要再等待多久温度才会升高的天数。如果之后都不会升高,请输入 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示:气温 列表长度的范围是 [1, 30000]。每个气温的值的都是 [30, 100] 范围内的整数。
解题思路
维护一个递减栈,存储元素下标。
遍历温度列表,如果栈为空则直接入栈,如果栈非空,则比较栈顶元素与当前温度,如果当前元素小于等于栈顶元素则直接入栈,如果当前元素大于栈顶元素,则表明已经找到第一次升温的位置,则直接计算下标差并修改result,之后将栈顶元素出栈,并继续比较下一个栈顶元素与当前温度值,直至当前元素小于等于栈顶元素,将当前值入栈,继续上述流程直至遍历结束。
实际做的时候,result直接初始化全0,所以遍历结束直接返回result即可。否则需要将栈内剩余元素对应result中的位置全部置0(没有找到升温的点)。
代码如下:
1 | class Solution { |
练习:逆波兰表达式求值
根据逆波兰表示法,求表达式的值。
有效的运算符包括 +, -, *, / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
- 整数除法只保留整数部分。
- 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
1 | 输入: ["2", "1", "+", "3", "*"] |
示例 2:
1 | 输入: ["4", "13", "5", "/", "+"] |
示例 3:
1 | 输入: ["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"] |
解题思路
典型用栈解决问题,计算的中间结果需要入栈。
代码如下:
1 | class Solution { |
Stack and DFS 栈和深度优先搜索
深度优先搜索(DFS)是用于在树/图中进行遍历/搜索的另一种算法。
在树的遍历中,可以用DFS进行前序遍历、中序遍历和后序遍历,这三种遍历的共同特点是除非到达最深的节点,否则不会回溯。
DFS和BFS的区别:BFS永远不会深入探索,除非已经遍历过当前层级的所有节点。
通常使用递归来实现DFS。
栈和DFS
DFS也可以用于查找从根节点到目标节点的路径。
(BFS是可以直接找到最短路径。)
如图所示:
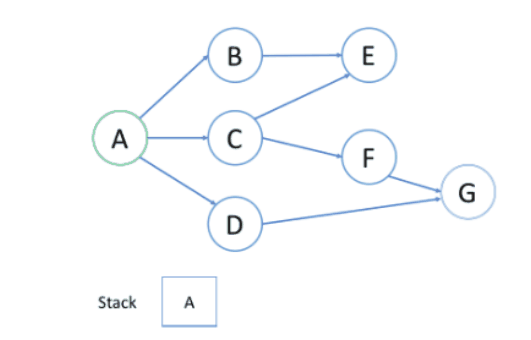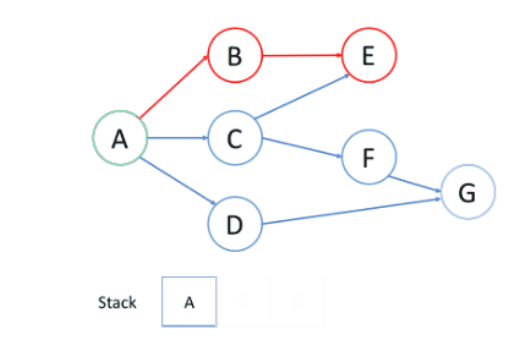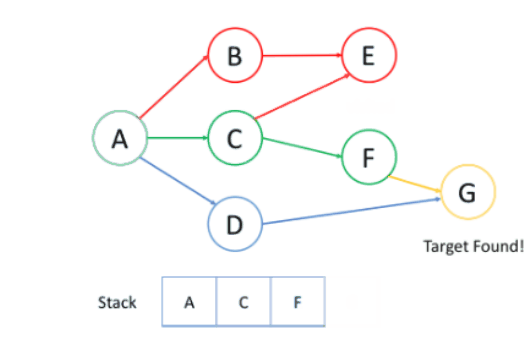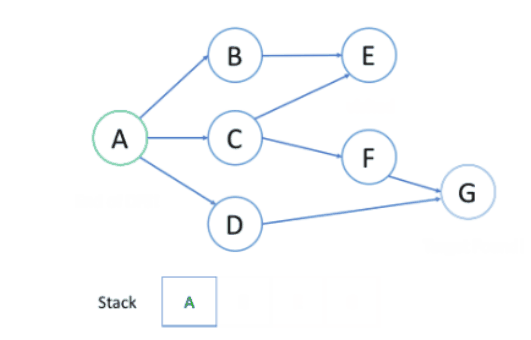
在上述例子中:
首先选择节点B的路径,到达E后无法深入,故回溯到A;再次选择节点C的路径,从C开始首先到达E,但E访问过,故回到C,并尝试F,最后找到了G。
DFS中找到的第一条路径不一定是最短的路径。
节点的处理和回溯过程是后进先出的处理顺序,和栈相同,故在DFS中多用栈来实现。
DFS-模板1
大多可以使用BFS的情况也可以使用DFS,区别主要在遍历顺序。
BFS找到的第一条路径为最短路径,而DFS不一定。
有两种实现DFS的方法,第一种为递归。
伪代码如下:
1 | /* |
使用递归实现DFS时,使用的是系统提供的隐式栈,也称为call stack。
在每个堆栈元素中,都有一个当前值,一个目标值,一个访问过的数组的引用,和一个对数组边界的引用,这些就是DFS函数中的参数。栈的大小是DFS的深度,所以最坏情况下,维护系统占需要$O(h)$,其中$h$是DFS的最大深度。
在计算空间复杂度时,要记得考虑系统栈。
练习:岛屿的个数
给定一个由 '1'(陆地)和 '0'(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例 1:
1 | 输入: |
示例 2:
1 | 输入: |
解题思路
之前用BFS方法做过该题,主要是先遍历当前节点相邻的所有节点,之后继续查找下一个为’1’的点,重复上述过程。
此处用DFS方法递归遍历。
首先建立visited数组来记录某个位置是否访问过,对于为’1’且未曾访问过的位置,递归进入其上下左右位置上为’1’且未访问过的点,将其visited置为true,并继续进入其相连的相邻位置,直至周围没有为’1’的点,如此可将整个连通区域中所有的数都找到,将count数加一。之后再寻找下一个为’1’且未访问过的点,重复上述过程,直至遍历完整个grid数组。
代码如下:
1 | // DFS |
练习:克隆图
给定无向连通图中一个节点的引用,返回该图的深拷贝(克隆)。图中的每个节点都包含它的值 val(Int) 和其邻居的列表(list[Node])。
示例:
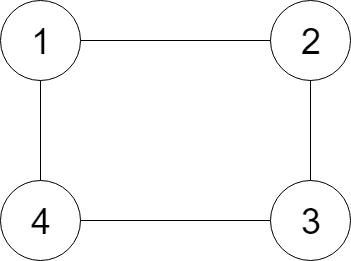
1 | 输入: |
提示:
- 节点数介于 1 到 100 之间。
- 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点 p 是节点 q 的邻居,那么节点 q 也必须是节点 p 的邻居。
- 必须将给定节点的拷贝作为对克隆图的引用返回。
解题思路
基本是图的遍历问题,使用DFS方法解答,要注意深度拷贝每个节点后,还要将其neighbors放到一个vector中,要注意避免重复拷贝。题意明确所有节点值不同,所以可使用map来存储已经拷贝过的节点(原节点和新的克隆节点一一对应)。
在递归函数中,首先判断节点是否为空,再看当前节点是否已经克隆过,若在map中存在则已经克隆过,直接返回其映射节点。否则就克隆当前节点,并在map中建立映射,并遍历该节点的所有neighbor节点,递归调用并实时更新map即可。
代码如下:
1 | /* |
练习:目标和
给定一个非负整数数组,a1, a2, …, an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例 1:
1 | 输入: nums: [1, 1, 1, 1, 1], S: 3 |
注意:
- 数组的长度不会超过20,并且数组中的值全为正数。
- 初始的数组的和不会超过1000。
- 保证返回的最终结果为32位整数。
解题思路
从第一个数字开始,调用递归函数,分别计算加当前值和减当前值之后的和,到数组结束时,比较当前和和目标值是否相等。(开始看网上的方法用目标和加/减当前值做递归的目标值来计算,结果在某个测试用例时提示超过int范围,,,)
参考测试用例:
1 | [1,1,1,1,1] |
代码如下:
1 | class Solution { |
中文版LeetCode提交上述代码时提示在上面第三个测试用例下超时,,,
使用数组记录中间值以减少重复计算。
代码如下:
1 | class Solution { |
DFS-模板2
递归虽然容易实现,但如果深度太高,容易栈溢出。这时可能希望使用BFS,或者用显式栈来实现DFS。
显式栈模板:
1 | /* |
这种方法使用while和栈来模拟递归时的系统调用栈。
练习:二叉树的中序遍历
给定一个二叉树,返回它的中序 遍历。
示例:
1 | 输入: [1,null,2,3] |
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
解题思路
中序遍历:先遍历左子树,然后访问值,再遍历右子树。
代码如下:
1 | /** |
小结
队列
队列是FIFO的数据结构,首先处理第一个元素;
队列两个重要操作:入队和出队;
可以用带有两个指针的动态数组来实现队列;
BFS方法常使用队列结构;
栈
栈是LIFO的数据结构,首先处理最后一个元素;
栈两个重要操作:push和pop;
使用动态数组可以实现栈;
DFS是栈的一个重要应用。
练习:用栈实现队列
使用栈实现队列的下列操作:
- push(x) — 将一个元素放入队列的尾部。
- pop() — 从队列首部移除元素。
- peek() — 返回队列首部的元素。
- empty() — 返回队列是否为空。
示例:
1 | MyQueue queue = new MyQueue(); |
说明:
- 你只能使用标准的栈操作 — 也就是只有
push to top,peek/pop from top,size, 和is empty操作是合法的。 - 你所使用的语言也许不支持栈。你可以使用 list 或者 deque(双端队列)来模拟一个栈,只要是标准的栈操作即可。
- 假设所有操作都是有效的 (例如,一个空的队列不会调用 pop 或者 peek 操作)。
解题思路
栈后进先出,队列先进先出。所以,在push的时候,借用一个额外的临时栈,首先将队列内原有元素挨个pop到临时栈(临时栈的顺序和构造的队列内顺序相反),再将新值push到临时栈,此时临时栈和要构造的队列元素顺序相反,新值在尾端。最后将临时栈再挨个pop到要构造的队列(实际也是用栈实现的)中,达到元素逆序的目的。
代码如下:
1 | class MyQueue { |
练习:用队列实现栈
使用队列实现栈的下列操作:
- push(x) — 元素 x 入栈
- pop() — 移除栈顶元素
- top() — 获取栈顶元素
- empty() — 返回栈是否为空
注意:
- 你只能使用队列的基本操作— 也就是
push to back,peek/pop from front,size, 和is empty这些操作是合法的。 - 你所使用的语言也许不支持队列。 你可以使用 list 或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
- 你可以假设所有操作都是有效的(例如, 对一个空的栈不会调用 pop 或者 top 操作)。
解题思路
和用栈实现队列的思路类似,push过程借用一个临时队列。需要注意的是,队列先入先出,所以此处要实现栈后入先出的目的,push的新值需要先插入临时队列,以保证pop时后插入的值可以先出去。
代码如下:
1 | class MyStack { |
练习:字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例:
1 | s = "3[a]2[bc]", 返回 "aaabcbc". |
解题思路
用栈,类似括号匹配,发现右括号时,开始出栈直至发现左括号,获取括号中要重复的内容,再出栈一次获取重复次数,之后将该字段重复指定次数后再入栈,直至遍历结束。将栈内容出栈,并按照指定顺序拼接成结果字符串返回即可。
注意的是,重复次数可能不是一位数字,所以在入栈时,对于连续的数字要拼接到一起再入栈。
使用的几个测试用例:
1 | "3[a]2[bc]" |
代码如下:
1 | class Solution { |
练习:图像渲染
有一幅以二维整数数组表示的图画,每一个整数表示该图画的像素值大小,数值在 0 到 65535 之间。
给你一个坐标 (sr, sc) 表示图像渲染开始的像素值(行 ,列)和一个新的颜色值 newColor,让你重新上色这幅图像。
为了完成上色工作,从初始坐标开始,记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点,接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点,……,重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。
最后返回经过上色渲染后的图像。
示例 1:
1 | 输入: |
注意:
image和image[0]的长度在范围[1, 50]内。- 给出的初始点将满足
0 <= sr < image.length和0 <= sc < image[0].length。 image[i][j]和newColor表示的颜色值在范围[0, 65535]内。
解题思路
和前面岛屿的个数类似,主要找到与初始点颜色相同且相连的节点,将其着色返回即可。
采用BFS或DFS递归均可,此处使用BFS,首先初始点标记访问、修改颜色、入队,后遍历其相邻节点,将颜色相同的相邻点标记访问、修改颜色、入队。直至队列为空,说明与初始点相连接的所有点均遍历结束,则返回。
代码如下:
1 | class Solution { |
练习:01矩阵
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
示例 1:
输入:
1 | 0 0 0 |
输出:
1 | 0 0 0 |
示例 2:
输入:
1 | 0 0 0 |
输出:
1 | 0 0 0 |
注意:
- 给定矩阵的元素个数不超过 10000。
- 给定矩阵中至少有一个元素是 0。
- 矩阵中的元素只在四个方向上相邻: 上、下、左、右。
解题思路
找到最近的0的距离,是最短路径问题,用BFS。
类比前面 walls and gates ,首先将原矩阵中所有值为0的点入队,值为1的点设为无限大INT_MAX(为了后续比较最小距离)。
遍历queue中节点的相邻节点,若该相邻节点的值大于当前节点值加1,则将其修改为当前值加1,且将该相邻节点入队,否则跳过(当相邻节点距离更小的时候,不需要更新),直至队列为空结束。
代码如下:
1 | class Solution { |
练习:钥匙和房间
有 N 个房间,开始时你位于 0 号房间。每个房间有不同的号码:0,1,2,...,N-1,并且房间里可能有一些钥匙能使你进入下一个房间。
在形式上,对于每个房间 i 都有一个钥匙列表 rooms[i],每个钥匙 rooms[i][j] 由 [0,1,...,N-1] 中的一个整数表示,其中 N = rooms.length。 钥匙 rooms[i][j] = v 可以打开编号为 v 的房间。
最初,除 0 号房间外的其余所有房间都被锁住。
你可以自由地在房间之间来回走动。
如果能进入每个房间返回 true,否则返回 false。
示例 1:
1 | 输入: [[1],[2],[3],[]] |
示例 2:
1 | 输入:[[1,3],[3,0,1],[2],[0]] |
提示:
1 <= rooms.length <= 10000 <= rooms[i].length <= 1000- 所有房间中的钥匙数量总计不超过
3000。
解题思路
用栈实现,并且维护一个长度N的数组标记房间是否能够打开。
首先将0号房间的钥匙全部入栈,之后挨个出栈,并且判断当前的钥匙对应的房间是否已经打开,如果已经打开就跳过,如果是第一次打开,就将该房间的钥匙入栈,并标记该房间。
到栈为空时,如果标记房间的数组值全为true,则返回true,否则返回false。
同样的思路,用队列也可以,队列是BFS,栈的话就是DFS。
代码如下:
1 | class Solution { |