【LeetCode】119、杨辉三角2

119、Pascal’s Triangle II杨辉三角2

难度：简单

题目描述

英文：

Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal’s triangle.

Note that the row index starts from 0.
中文：

给定一个非负索引 k，其中 k ≤ 33，返回杨辉三角的第 k 行。

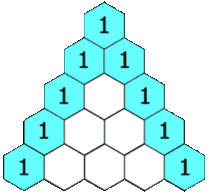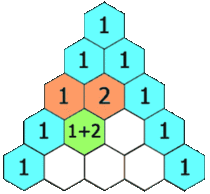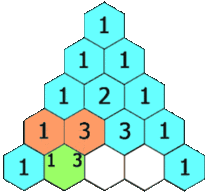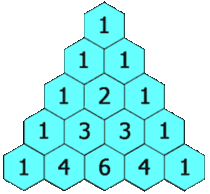
在杨辉三角中，每个数是它左上方和右上方的数的和。
示例

Example:
1
2
Input: 3
Output: [1,3,3,1]
进阶

你可以优化你的算法到 O(k) 空间复杂度吗？

解题思路

思路一

进行Recursion探索时完成的，其他解法后续补充。

递归关系

我们从定义杨辉三角的递归关系开始。

首先，定义函数$f(i,j)$，表示杨辉三角中第$i$行$j$列的值，之后可以将递归关系表示如下：

$f(i,j)=f(i-1,j-1)+f(i-1,j)$

基本情况

在杨辉三角中，每行的最左和最右数字是这个问题的基本情况，值总是为1.

所以，我们可以定义基本情况如下：

$f(i,j)=1\qquad where\qquad j=1\ or\ j=i$

代码没有完全对应Recursion相应位置的方法，实现过程中，采用自底向上的方法，保存前一行的中间结果。

代码上注意一下，此处的rowIndex从0开始。

代码提交

C++，用时4ms，内存8.3M

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> temp;
        temp.push_back(1);

        if (rowIndex == 0) {
            return temp;
        }

        vector<int> result;
        for (int row = 1; row <= rowIndex; row++) {
            result.clear();
            for (int col = 0; col <= row; col++) {
                if (col == 0 || col == row) {
                    result.push_back(1);
                }
                else {
                    result.push_back(temp[col - 1] + temp[col]);
                }
            }
            temp = result;
        }
        return result;
    }
};

思路二

和思路一类似，先开辟一个大小为$k$的空间，保留每次前一行的中间结果，在其基础上直接修改获取当前行的结果。

修改过程中，先填充当前行的末尾值（比前一行最末的位置+1位），然后从右往左依次修改，当前行位置为$j$的值，仅依赖于上一行位置为$j-1$和$j$的值，所以，逆序修改的过程中，改掉的值都是下一步计算不再需要的值。

代码提交

C++，用时4ms，内存8.3M

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> res(rowIndex + 1);	// 长度为K，默认值为0
        res[0] = 1;
        for (int i = 1; i <= rowIndex; ++i) {	// 从第1行开始（从0开始数）计算每一行的参数
            for (int j = i; j >= 1; --j) {
                res[j] += res[j - 1];	// 更新j位置上的数为上一行的j-1位置与j位置的数的和，最末端为 0+上一行最末端
            }
        }
        return res;
    }
};