【LeetCode】Explore：Recursion I 递归—1

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：

主要翻译自LeetCode上Explore模块的Recursion I，有直译，也有非直译的个人理解。

其中涉及的题目附有相应的解答。

Overview 综述

Recursion（递归）是计算机科学中一个重要的概念，是很多算法和数据结构的基础。但是对于很多初学者都比较难把握。

在开始本节探索之前，我们强烈建议先完成二叉树和堆栈两个探索页。

在这个探索页，我们将回答以下几个问题：

  1. 什么是recursion？它是如何工作的？
  2. 如何递归的解决一个问题？
  3. 如何分析递归算法的时间和空间复杂度（time and space complexity）？
  4. 如何更好的应用递归？

完成本探索页后，你在解决递归问题和分析复杂度时会变得更加自信。

一、Principle of Recursion 递归原理

在这章，我们将会：

  1. 解释递归的基本概念；
  2. 演示如何应用递归解决确切的问题；
  3. 最后提供一些练习题来练习递归；

递归原理

递归是一种将函数本身作为子程序调用来解决问题的方法。

你可能想知道一个函数怎样调用其自身。诀窍在于每次递归的调用其本身时，都将给定的问题缩小成其子问题，这样持续的递归调用，直到子问题可以不用递归就能解决的时候停止。

一个递归函数应该有以下属性，这样才不会导致无限循环：

  1. 具有简单的基本情况，即递归出口、递归结束条件，即不使用递归即可获得答案的情况；
  2. 一系列规则，称为recurrence relation递归关系，可以将问题逐步缩小直至递归出口；

注意，可能会有多个可以调用函数本身的地方。

示例

从一个简单的问题开始：逆序输出字符串。

倒序输出一个字符串。

你可以很容易的迭代解决这个问题，例如从字符串的结尾开始遍历字符串。但是如何递归的解决呢？

首先，我们定义函数printReverse(str[0...n-1])，其中str[0]表示字符串的第一个字符，然后我们通过以下两个步骤解决这个问题：

  1. printReverse(str[1...n-1])：逆序输出子串strp[1...n-1]；
  2. print(str[0])：输出字符串的首字符；

我们在第一步中定义了递归关系。

代码如下（C++）：

1
2
3
4
5
6
void printReverse(const char *str) {
    if (!*str)
        return;
    printReverse(str+1);
    cout << *str;
}

接下来，来处理一个和示例略有不同的练习，尽量用递归来解决。

练习：反转字符串

【LeetCode】344、Reverse String

写一个反转字符串的函数，输入字符数组char[]。

不要开辟额外的控件，必须使用$O(1)​$的空间复杂度就地修改输入的数组。

假定所有的字符都是可打印的ASCII码字符。

Example 1:

1
2
Input: ["h","e","l","l","o"]
Output: ["o","l","l","e","h"]

Example 2:

1
2
Input: ["H","a","n","n","a","h"]
Output: ["h","a","n","n","a","H"]

递归代码如下（自己写的，C++）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    void swap(vector<char>& s, int left, int right) {
        if (left >= right) {
            return;
        }
        char temp = s[left];
        s[left] = s[right];
        s[right] = temp;
        swap(s, left+1, right-1);
        return;
    }
    
    void reverseString(vector<char>& s) {
        if (s.size() <= 1)
            return;
        swap(s, 0, s.size()-1);
        return;
    }
};

解答：反转字符串

本章，我们给出反转字符串问题的一个简单的解决方案。

问题并不难，关键在于有一个额外的约束条件，即使用$O(1)$的额外空间进行修改。

定义函数reverseString(str[0...n-1])，其中str[0...n-1]是一个首字符为str[0]的字符数组。

下面，我们讨论如何利用递归的思想来解决这个问题。

初次尝试

如果我们按照上文逆序输出字符串的思路，我们可以有以下的方法：

  1. 从输入字符串中取首字符str[0]；
  2. 对于剩下的子字符串，调用函数自身来递归解决，如reverseString(str[1...n-1])；
  3. 在步骤2返回的结果中添加首字符；

这个方法可以实现题意效果，但是不满足约束条件。因为需要额外的空间来保存步骤2的中间结果，所需空间大小和字符串长度成正比（即需要$O(n)$的空间复杂度），这一点不满足$O(1)$空间复杂度的要求。

另一种分治的方法

考虑题目中的约束条件，将其放入到递归的问题中，可以理解为在两次连续的递归调用之间不使用额外的空间消耗，也就是说，我们应该把问题分解成独立的子问题。

分解成独立子问题的一个思路是将每次输入的字符串分成两部分：1、首尾字符；2、去掉首位字符后剩下的子字符串。然后可以独立的解决两部分内容。

按照上述方法，可以有以下的方法：

  1. 从输入的字符串中取首尾字符str[0]和str[n-1]；
  2. 就地交换首尾字符；
  3. 递归调用函数来反转剩余的子字符串，即reverseString(str[1...n-2])；

注意：步骤2、3可以交换，因为是两个独立的任务。但最好保持现状的顺序，这样可以使用尾递归优化调用。我们会在后面的章节详细了解尾递归。（先简单理解一下，尾递归是指函数运行的最后一步是调用其自身，尾递归由于递归在最后一步，不再需要考虑外层函数的信息，因此可以把这个函数的调用栈给优化掉，从而避免栈溢出的风险。）

代码如下（示例代码，Python3）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def reverseString(self, s):
        """
        :type s: List[str]
        :rtype: void Do not return anything, modify s in-place instead.
        """
        def helper(start, end, ls):
            if start >= end:
                return
        
            # swap the first and last element
            ls[start], ls[end] = ls[end], ls[start]        

            return helper(start+1, end-1, ls)
    
        helper(0, len(s)-1, s)

如图，用字符数组["h", "e", "l", "l", "o"]举例，可以看到如何进行分解并解决的。

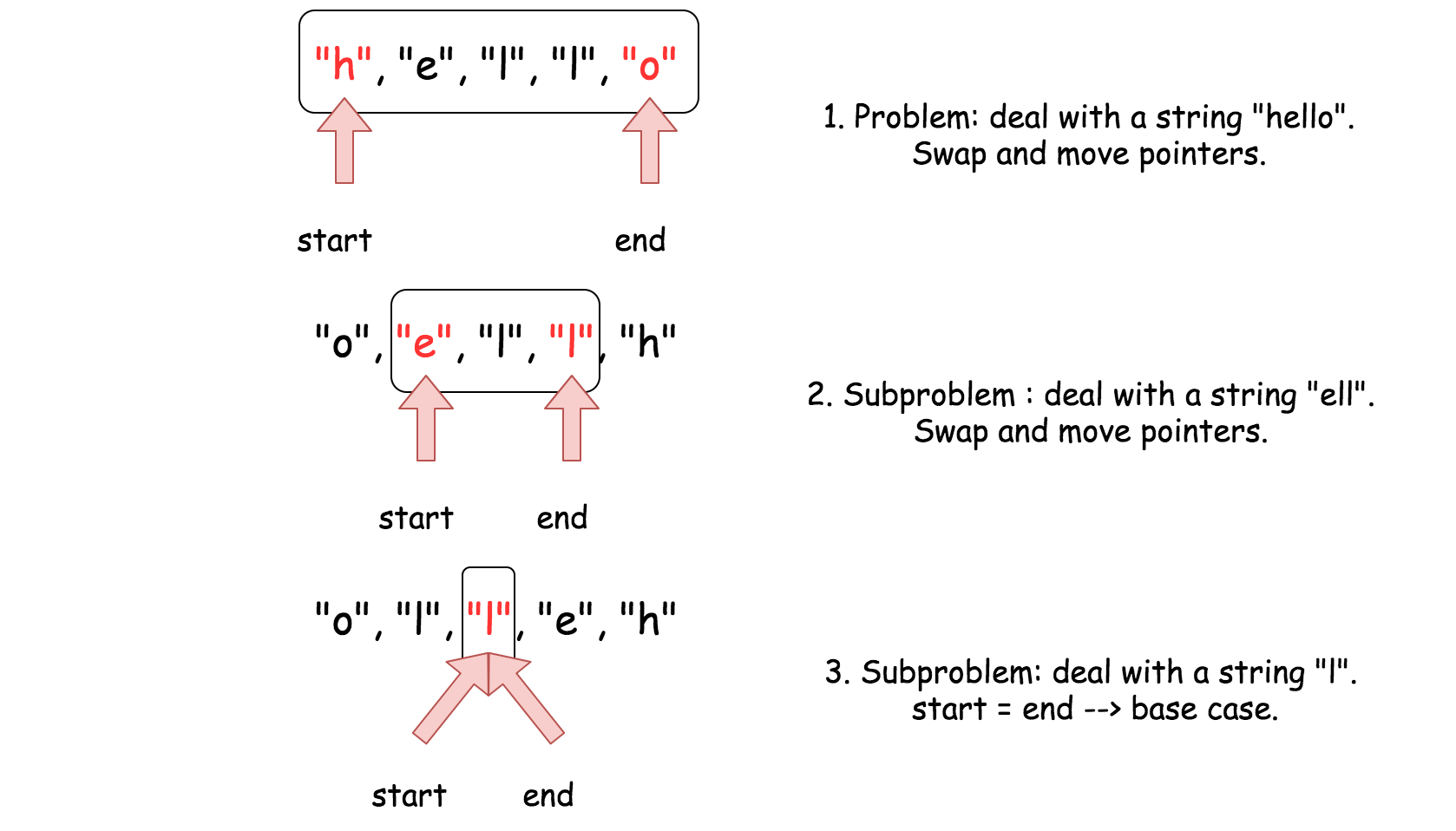
使用这种方法，在每次递归调用的时候只需要常数级内存空间用来交换首尾字符即可，满足题目的约束条件。

递归函数

对于一个问题而言，如果可以用递归的思路来解决的话，那我们一定可以遵循如下的思路来实现。

举例来说，我们用一个待实现的函数$F(X)$来表示问题，其中$X$表示函数的输入，也就是问题的范围。

那么，在函数$F (X)$中，我们将做如下操作：

  1. 把问题分解为更小的范围，如$x_0\in X , x_1\in X , … , x_n\in X$；
  2. 递归调用函数$F(x_0),F(x_1),…,F(x_n)$来解决$X$的子问题；
  3. 最后，处理递归调用的结果，从而解决$X$对应的问题；

举例

通过递归解决另一个问题来展示上述思路。

给定一个链表，交换其中每两个相邻节点，并返回头结点。

例如：给定列表1->2->3->4，应该返回交换后的列表2->1->4->3的头结点。

定义函数swap(head)，其中输入参数head表示链表的头结点。函数应该返回相邻节点交换后的新链表的头结点。

按照上述思路，我们可以按如下步骤实现这个函数：

  1. 首先，我们交换链表的前两个节点，即head和head.next；
  2. 然后，我们递归调用函数swap(head.next.next)来处理链表的剩余部分；
  3. 最后，获得步骤2返回的子链表的头结点，并将其和步骤1的新链表相连接；

作为练习，可以按照上文提供的步骤试着实现该问题的完整代码。

练习：两两交换链表中的节点

详见【LeetCode】24、Swap Nodes in Pairs

Swap Nodes in Pairs

Given a linked list, swap every two adjacent nodes and return its head.

You may not modify the values in the list’s nodes, only nodes itself may be changed.

给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

Example:

1
Given 1->2->3->4, you should return the list as 2->1->4->3.

代码如下（C++，用时4ms，内存9M）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (!head || !head->next) return head;
        ListNode *t = head->next;
        head->next = swapPairs(head->next->next);
        t->next = head;
        return t;
    }
};

二、Recurrence Relation 递归关系

上一章我们了解了递归的基本概念。

在实现递归函数之前，有两个重要的点需要注意：基本情况和递归关系。

在这章，我们将：

  • 通过详细的例子来了解如何定义基本情况和递归关系；
  • 做一些练习；

递归关系

在实现递归函数之前，要注意两个重要的点：

  • 递归关系：总问题结果和子问题结果之间的关系；
  • 基本情况：不需要继续递归调用就能够计算结果的情况，就是递归结束情况。（有时基本情况也被叫做bottom cases，因为如果我们用自顶向下的方式对问题进行分解的话，那么基本情况通常出现在问题已经被分解到最小范围的时候，即bottom）

一旦我们有了上述两方面内容，那么我们只需要按照递归关系不断的调用函数本身，直到到达基本情况。

为了解释上述内容，我们来看一个经典问题：杨辉三角（也叫 帕斯卡三角）。

杨辉三角是由一系列数字组成的三角形。其中，每一行的最左边和最右边永远是1，剩余的其他数字，每个数是其上面两个数的和。

示例：杨辉三角

下图是一个五层的杨辉三角示意图：

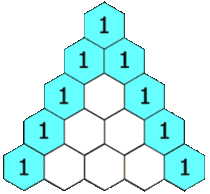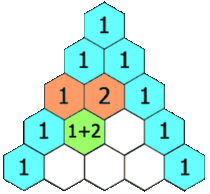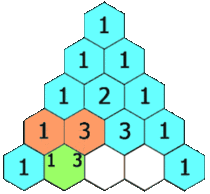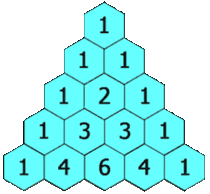
基于以上定义，我们的问题就是生成指定层数的杨辉三角。

递归关系

我们从定义杨辉三角的递归关系开始。

首先，定义函数$f(i,j)$，表示杨辉三角中第$i$行$j$列的值，之后可以将递归关系表示如下：

基本情况

在杨辉三角中，每行的最左和最右数字是这个问题的基本情况，值总是为1.

所以，我们可以定义基本情况如下：

示例

可以看到，一旦定义了递归关系和基本情况之后，就可以很直观的实现递归函数了，特别是定义好数学公式以后。

如下是应用上述公式计算$f(5,3)$，即第5行第3列的值的过程。

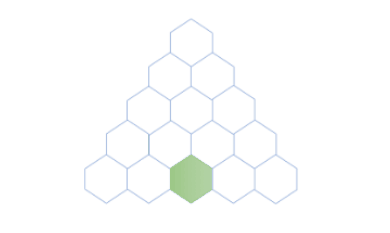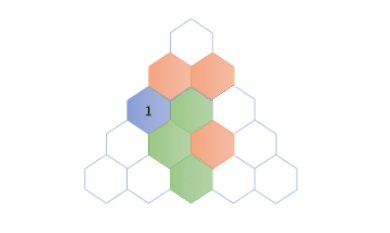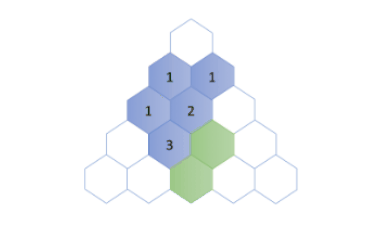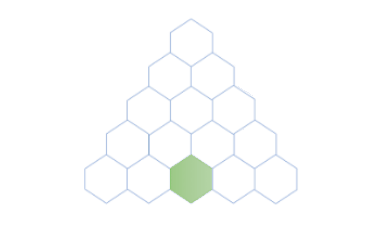
要计算$f(5,3)$，我们按照递归关系将问题分解$f(5,3)=f(4,2)+f(4,3)$，之后递归计算$f(4,2)$和$f(4,3)$的值：

  • 对于$f(4,2)$，我们可以继续分解，直至基本情况，如下所示：

  • 对于$f(4,3)$，同样的，我们可以将其分解如下：

  • 最后我们组合上述子问题的结果：

下一步

在上面的示例中，可以注意到在递归解决方案中有一些重复的计算，就是说，我们为了计算最后一行的值，重复的计算了很多中间结果。例如，为了计算$f(5,3)$，我们在计算$f(4,2)$和$f(4,3)$的过程中重复计算了两边$f(3,2)$的值。

我们将在下一章讨论如何避免这些重复计算。

按照本章的内容，可以做一些和杨辉三角相关的练习题。

详见【LeetCode】118、杨辉三角，【LeetCode】119、杨辉三角2，【LeetCode】206、反转链表。

练习：杨辉三角

Pascal’s Triangle

Given a non-negative integer numRows, generate the first numRowsof Pascal’s triangle.

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

示例:

1
2
3
4
5
6
7
8
9
输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

代码如下（C++，用时4ms，内存8.8M）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:    
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> result;
        if (numRows <= 0)
            return result;
        vector<int> temp;
        if (numRows == 1) {
            temp.push_back(1);
            result.push_back(temp);
            return result;
        }

        temp.push_back(1);
        result.push_back(temp);
        for (int row = 1; row < numRows; row++) {
            temp.clear();
            for (int col = 0; col <= row; col++) {
                if (col == 0 || col == row) {
                    temp.push_back(1);
                }
                else {
                    temp.push_back(result[row - 1][col - 1] + result[row - 1][col]);
                }
            }
            result.push_back(temp);
        }
        return result;
    }
};

练习：杨辉三角2

Pascal’s Triangle II

Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal’s triangle.

Note that the row index starts from 0.

Example:

1
2
Input: 3
Output: [1,3,3,1]

Follow up:

Could you optimize your algorithm to use only O(k) extra space?

代码如下（C++，用时4ms，内存8.3M）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> temp;
        temp.push_back(1);

        if (rowIndex == 0) {
            return temp;
        }

        vector<int> result;
        for (int row = 1; row <= rowIndex; row++) {
            result.clear();
            for (int col = 0; col <= row; col++) {
                if (col == 0 || col == row) {
                    result.push_back(1);
                }
                else {
                    result.push_back(temp[col - 1] + temp[col]);
                }
            }
            temp = result;
        }
        return result;
    }
};

练习：反转链表

Reverse Linked List

Reverse a singly linked list.

Example:

1
2
Input: 1->2->3->4->5->NULL
Output: 5->4->3->2->1->NULL

Follow up:

A linked list can be reversed either iteratively or recursively. Could you implement both?

代码如下（C++，用时8ms，内存9M）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* reverse(ListNode* pre, ListNode* cur) {
        if (cur->next == NULL) { // 递归结束的判断
            cur->next = pre;
            return cur;
        }
        ListNode* next = cur->next;
        cur->next = pre;
        pre = cur;
        cur = next;
        return reverse(pre, cur);
    }
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = NULL, *cur = head;
        return head ? reverse(pre, cur) : head; // 如果head为空的话，我们直接返回head/NULL
    }
};

解答：反转链表

方法1、迭代法

假设有链表$1\rightarrow 2\rightarrow 3\rightarrow \emptyset$，要将其转为$\emptyset \leftarrow 1\leftarrow 2\leftarrow 3$。

遍历链表，将当前节点的next指针指向其前一个节点。由于链表没有指向前一个节点的指针，所以需要提前保存前一个节点的信息。同时还需要一个指针，在改变next指向时用来保存当前next的节点。最后不要忘了返回新的头结点。

1
2
3
4
5
6
7
8
9
10
11
public ListNode reverseList(ListNode head) {
    ListNode prev = null;
    ListNode curr = head;
    while (curr != null) {
        ListNode nextTemp = curr.next;
        curr.next = prev;
        prev = curr;
        curr = nextTemp;
    }
    return prev;
}

复杂度分析

  • 时间复杂度：$O (n)$。$n$是链表长度。
  • 空间复杂度：$O (1)$。

方法2、递归法

递归方法要考虑回退工作，略难一点。假设链表的剩余部分已经反转好了，怎么反转其前半部分呢？

对于链表$n_1\rightarrow …\rightarrow n_{k-1} \rightarrow n_k \rightarrow n_{k+1} \rightarrow … \rightarrow n_m \rightarrow \emptyset​$，假设从节点$n_{k+1}​$到节点$n_m​$已经反转好了，并且当前在节点$n_k​$处：$n_1 \rightarrow … \rightarrow n_{k-1} \rightarrow \mathbf{n_k} \rightarrow n_{k+1} \leftarrow … \leftarrow n_m​$。

我们想让$n_{k+1}$的下一个节点指向$n_k$，所以：$n_k .next.next=n_k$。

要注意的是$n_1$节点的next必须指向$\emptyset​$。如果忽略这一步的话，那就把链表变成首尾相接的圆形的了。如果测试链表长度为2的情况，可能会触发这个bug。

1
2
3
4
5
6
7
public ListNode reverseList(ListNode head) {
    if (head == null || head.next == null) return head;
    ListNode p = reverseList(head.next); // 保留头结点，递归反转剩余部分
    head.next.next = head; // 把剩余部分的头结点指向到保留的头结点上，类似上文说的 n(k+1) 的next指向到 nk ，实现反转
    head.next = null; // 把保留的头结点反转，指向空，即 n(k+1) 指向 nk 后，再将 nk 指向空
    return p;
}

复杂度分析

  • 时间复杂度：$O (n)$。$n$是链表长度。
  • 空间复杂度：$O(n)$。额外的空间消耗来源于递归所需的隐藏的栈空间，递归最深为$n$层。

三、Memoization 缓存计算

在上一章，我们提到过递归算法中的重复计算问题。在最好的情况下，重复计算只是会增加算法的时间复杂度，但是在最差的情况，重复计算会导致无限循环。

因此，在这章，我们将：

  • 用一个例子开始，展示重复计算是如何导致的；
  • 展示如何用缓存计算的技术来避免重复计算；

递归中的重复计算

递归是实现算法的一种强有力的方法，但是如果不好好使用的话，也会带来额外的问题，如重复计算。例如，在上一章的后半部分，我们提到过杨辉三角中的重复计算问题，一些中间结果被反复计算了多次。

在这章，我们将进一步的讨论递归中可能发生的重复计算问题，并提出一种叫做缓存计算的常用技术手段来避免这个问题。

为了用另一个例子来演示重复计算问题，我们看一个大部分都熟悉的例子：斐波那契数列。如果我们定义函数$F(n)$来表示索引为$n$的斐波那契数，那可以得到如下所示的递归关系式：

而基本情况（递归结束条件）为：

有了斐波那契数的定义之后，可以按如下所示实现代码：

1
2
3
4
5
6
7
8
9
def fibonacci(n):
    """
    :type n: int
    :rtype: int
    """
    if n < 2:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

现在，如果想计算$F(4)$，就可以按照上述公式来实现：

可以看到，按照上述过程，为了计算$F(4)$的结果，我们需要计算两遍$F(2)$。

如图所示，用一棵树展示了在计算$F(4)​$的过程中进行的所有重复计算（用颜色分类）：

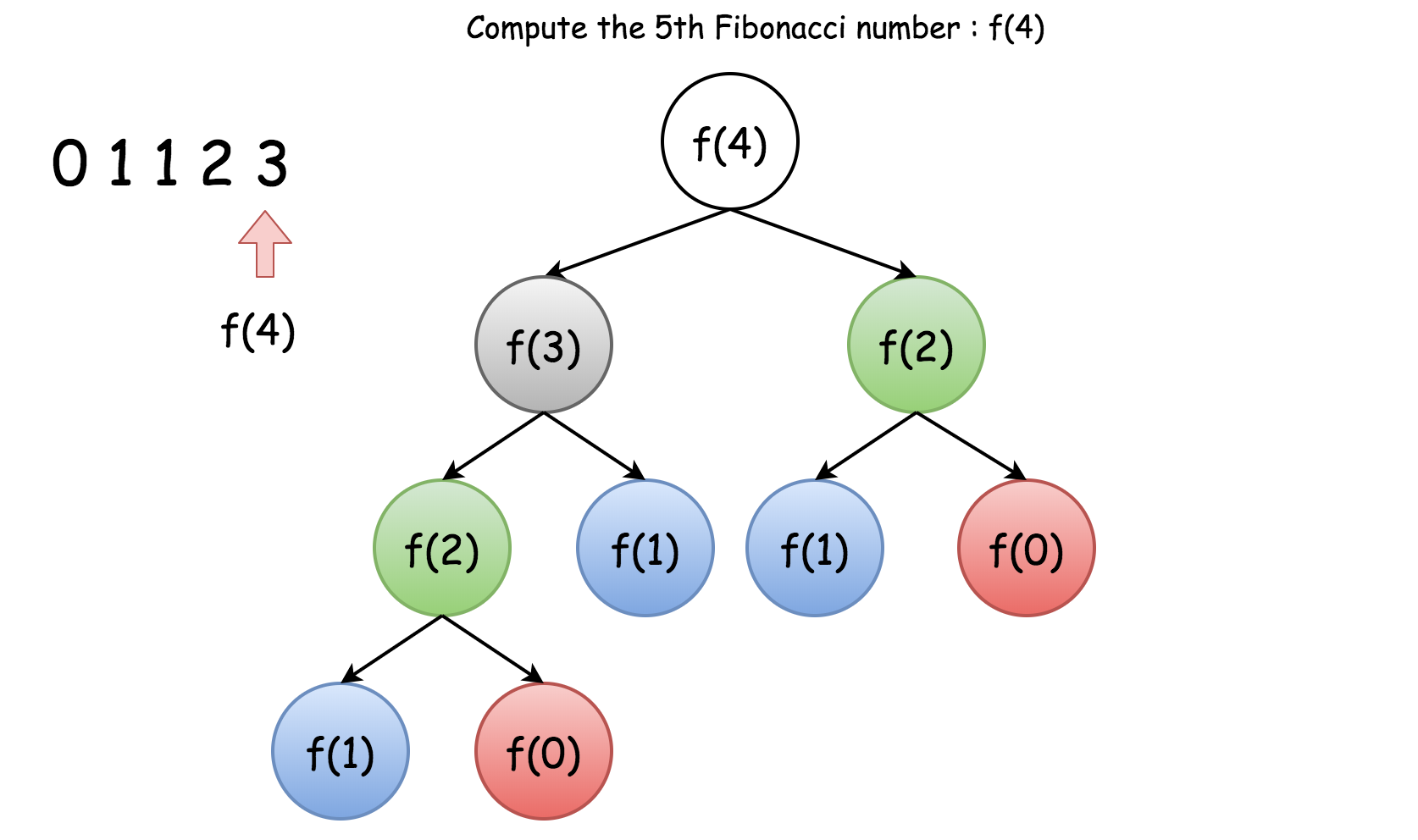
缓存计算

为了尽可能多的消除上述情况中的重复计算，一个方法就是将中间结果保存在缓存中，这样下次遇到的时候就可以重复使用而不需要再次计算了。

这个方法就是缓存计算方法，是经常和递归一起使用的一种技术。

Memoization is an optimization technique used primarily to speed up computer programs by storing the results of expensive function calls and returning the cached result when the same inputs occur again. (Source: wikipedia)

缓存计算是通过将高消耗的函数调用结果进行保存，并且在再次遇到相同输入的时候返回缓存结果，从而提升程序运行速度的一种优化技术。

回到斐波那契函数$F(n)$，我们可以用一个哈希表来跟踪每个$F(n)$的值，用$n$做key。哈希表作为缓存使我们避免重复计算。缓存技术是一个很好的用一些额外空间来换取时间减少的例子。

为了对比，我们提供了如下的用缓存计算实现的斐波那契数。

作为练习，可以通过更一般性的方法来实现缓存计算，即不改变原来的函数而应用缓存计算。（可以引用设计模式decorator）

关于decorator设计模式可参考设计模式——decorator

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def fib(self, N):
    """
    :type N: int
    :rtype: int
    """
    cache = {}
    def recur_fib(N):
        if N in cache:
            return cache[N]

        if N < 2:
            result = N
        else:
            result = recur_fib(N-1) + recur_fib(N-2)

        # put result in cache for later reference.
        cache[N] = result
        return result

    return recur_fib(N)

使用decorator模式代码如下（自己实现）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from functools import wraps

class Solution(object):
    def cache(func): 
        caches = {} 
        @wraps(func) 
        def wrap(*args): 
            if args not in caches: 
                caches[args] = func(*args)
            return caches[args] 
        return wrap 
    
    @cache 
    def fib(self, n): 
        """
        :type N: int
        :rtype: int
        """
        if n < 2: 
            return n
        return self.fib(n-1) + self.fib(n-2)

在这章中，可以通过斐波那契数和爬楼梯问题来进行练习。

详见：【LeetCode】509、斐波那契数，【LeetCode】70、爬楼梯

在下一章，我们将深入讨论在递归算法中的复杂度分析。

练习：斐波那契数

The Fibonacci numbers, commonly denoted F(n) form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from 0 and 1. That is,

1
2
F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), for N > 1.

Given N, calculate F(N).

Example 1:

1
2
3
Input: 2
Output: 1
Explanation: F(2) = F(1) + F(0) = 1 + 0 = 1.

Example 2:

1
2
3
Input: 3
Output: 2
Explanation: F(3) = F(2) + F(1) = 1 + 1 = 2.

Example 3:

1
2
3
Input: 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.

Note:

0 ≤ N ≤ 30.

代码如下（Python，用时20ms，内存11.8M）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution(object):
    def fib(self, N):
        """
        :type N: int
        :rtype: int
        """
        cache = {}
        def recur_fib(N):
            if N in cache:
                return cache[N]

            if N < 2:
                result = N
            else:
                result = recur_fib(N-1) + recur_fib(N-2)

            # put result in cache for later reference.
            cache[N] = result
            return result

        return recur_fib(N)

练习：爬楼梯

You are climbing a stair case. It takes n steps to reach to the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

Note: Given n will be a positive integer.

Example 1:

1
2
3
4
5
Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps

Example 2:

1
2
3
4
5
6
Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step

代码如下（Python3，用时80ms，内存13.2M）：

1
2
3
4
5
6
7
8
9
10
class Solution:
    def climbStairs(self, n: int) -> int:
        if n == 1:
            return 1
        if n == 2:
            return 2
        tempNum = [0,1,2]
        for i in range(3, n+1):
            tempNum.append(tempNum[i-1] + tempNum[i-2])
        return tempNum[n]

解答：爬楼梯

本节代码均为原网页给出的参考代码，均为Java实现。

方法1：暴力法

暴力法就是计算所有可能的走法组合，也就是每一步爬1层和每一步爬两层。在每一步我们都调用函数$climpStairs$来计算爬一层和爬两层的结果，并返回两个函数返回值的和。

其中$i$表示当前层数，$n$表示目标层数。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Solution {
    public int climbStairs(int n) {
        climb_Stairs(0, n);
    }
    public int climb_Stairs(int i, int n) {
        if (i > n) {
            return 0;
        }
        if (i == n) {
            return 1;
        }
        return climb_Stairs(i + 1, n) + climb_Stairs(i + 2, n);
    }
}

复杂度分析

  • 时间复杂度：$O(2^n)$。递归树的大小是$2^n$。

    如下所示为$n=5$时的递归树：

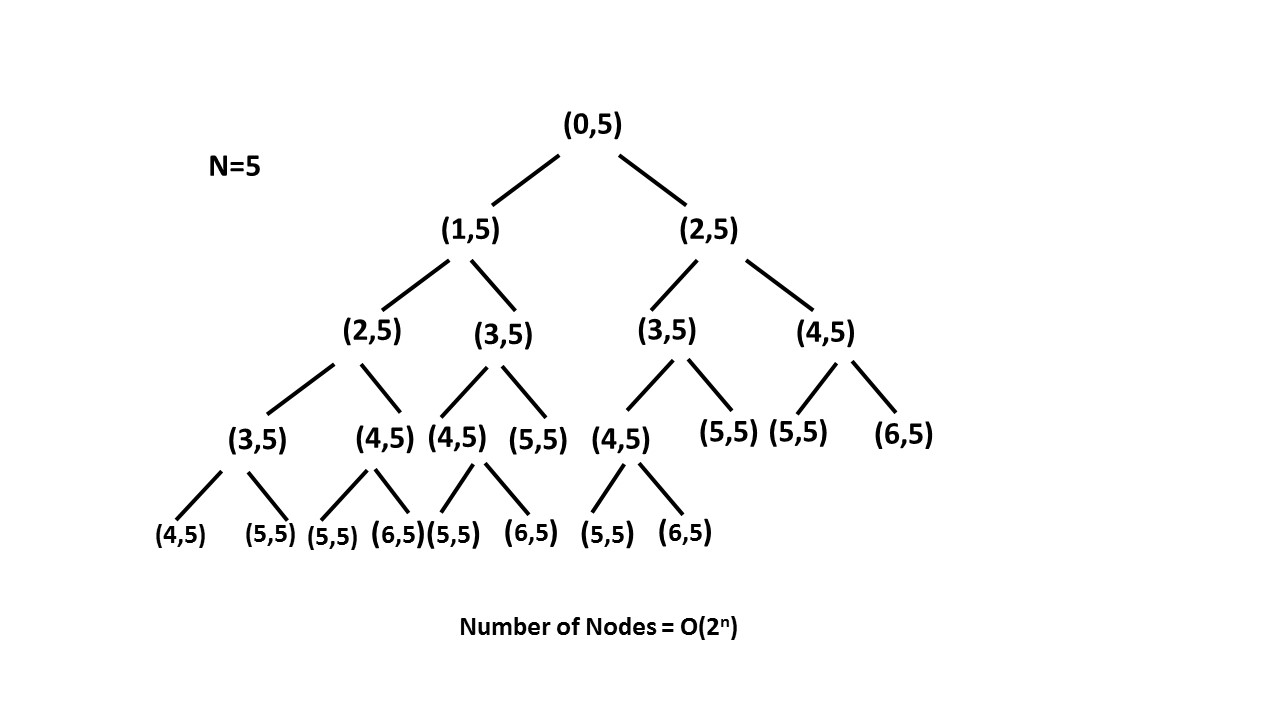
  • 空间复杂度：$O(n)$。递归树的最大深度为$n$。

方法2：采用缓存计算的递归法

在上一种方法中重复计算了很多中间结果。可以用一个memo数组将每一步的结果进行存储，当再次调用这个函数的时候可以直接从memo数组中返回结果。

通过这种使用memo数组来调整递归树的方法，可以将递归树的大小减少到$n$。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class Solution {
    public int climbStairs(int n) {
        int memo[] = new int[n + 1];
        return climb_Stairs(0, n, memo);
    }
    public int climb_Stairs(int i, int n, int memo[]) {
        if (i > n) {
            return 0;
        }
        if (i == n) {
            return 1;
        }
        if (memo[i] > 0) {
            return memo[i];
        }
        memo[i] = climb_Stairs(i + 1, n, memo) + climb_Stairs(i + 2, n, memo);
        return memo[i];
    }
}

复杂度分析

  • 时间复杂度：$O(n)$。递归树的大小为$n$。
  • 空间复杂度：$O(n)$。递归树的最大深度为$n$。

方法3：动态规划

可以看到，这个问题可以分解成多个子问题，并且包含最优子结构性质，也就是说，这个问题的最优解可以通过其子问题的最优解来组合得到，所以我们可以采用动态规划方法来解决这个问题。

我们可以通过以下两种方法到达第$i$层：

  1. 在第$i-1$层走一步；
  2. 在第$i-2$层走两步；

所以，到达第$i$层的总方法数等于到达第$i-1$层的方法数和到达第$i-2$层的方法数的总和。

用$dp[i]$表示到达第$i$层所需的总方法数，则：

例如：

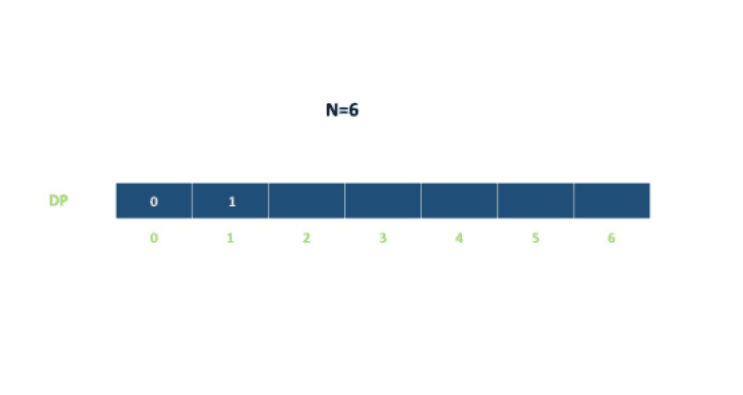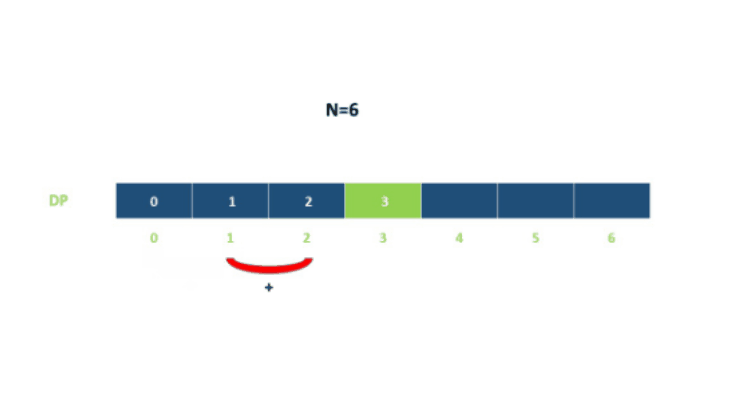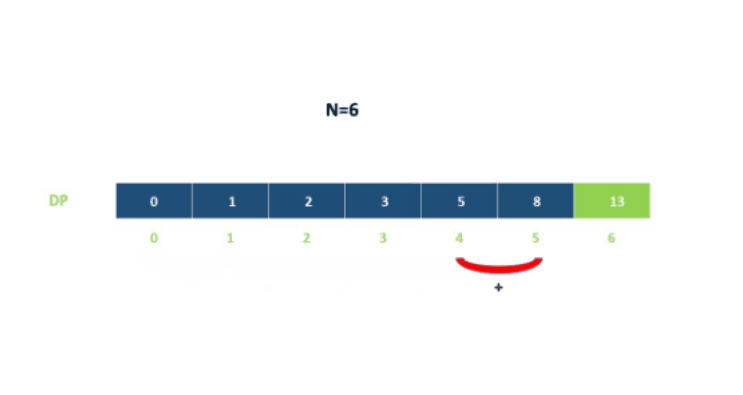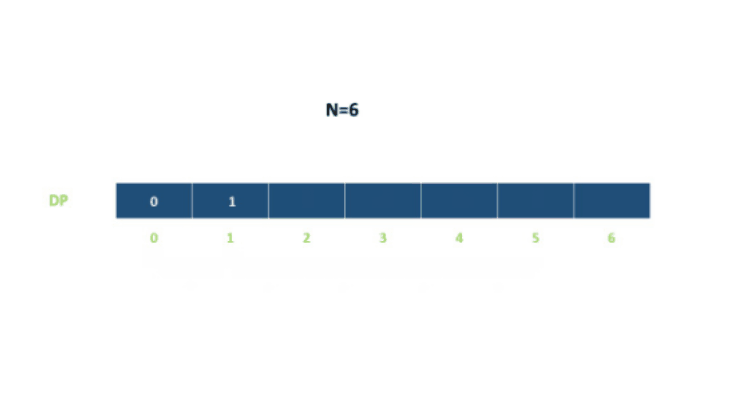
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Solution {
    public int climbStairs(int n) {
        if (n == 1) {
            return 1;
        }
        int[] dp = new int[n + 1];
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        return dp[n];
    }
}

复杂度分析

  • 时间复杂度：$O(n)$。单层循环到$n$。
  • 空间复杂度：$O(n)$。使用大小为$n$的$dp$数组。

方法4：斐波那契数法

在上面的方法中使用了$dp$数组，并且$dp[i]=dp[i-1]+dp[i-2]$。可以很容易的联想到，$dp[i]$正是斐波那契数的第$i$个值：

那么，我们只需要找到斐波那契数列的第$n$个值即可，其中前两个值分别为1和2，即$Fib(1)=1$，$Fib(2)=2$。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
    public int climbStairs(int n) {
        if (n == 1) {
            return 1;
        }
        int first = 1;
        int second = 2;
        for (int i = 3; i <= n; i++) {
            int third = first + second;
            first = second;
            second = third;
        }
        return second;
    }
}

复杂度分析

  • 时间复杂度：$O(n)$。计算第$n$个斐波那契数需要循环到$n$。
  • 空间复杂度：$O(1)$。使用固定的空间。

方法5：Binets Method （比奈法？）使用矩阵的方法

这是一个非常有趣的使用矩阵乘法来计算第$n$个斐波那契数的方法。矩阵形式如下：

令$Q= \begin{bmatrix}F_{n+1} & F_n \\ F_n & F_{n-1} \end{bmatrix}​$。按照这个方法，第$n​$个斐波那契数可以由$Q^{n-1}[0,0]​$得到。

我们来看方法的证明：

可以使用数学归纳法来证明这个方法。我们知道，这个矩阵给出了第3个斐波那契数（基本情况）的正确结果，$Q^2= \begin{bmatrix}2 & 1 \\ 1 & 1 \end{bmatrix}​$。这证明了基本情况是适用于这个方法的。

假设这个方法也适用于第$n$个斐波那契数的问题，即$F_n = Q^{n-1}[0,0]$，其中$Q^{n-1}= \begin{bmatrix} F_n & F_{n-1} \\ F_{n-1} & F_{n-2} \end{bmatrix}$。

现在，我们需要证明在上述两个条件为真的情况下，这个方法对于计算第$n+1​$个斐波那契数也是有效的，即证明$F_{n+1}=Q^n[0,0]​$。

证明过程：

所以，$F_{n+1}=Q^n[0,0]$。

至此，完成了这个方法的证明。

用这个方法解决爬楼梯问题所要做的唯一的改动就是，修改初始值为2和1（斐波那契数列的初始值是1和0）。或者，另一个方法是不修改初始值，而是使用相同的矩阵，但是用结果$result=Q^n[0,0]$来得到爬楼梯问题的第$n$层最终解。做这种调整的原因是因为爬楼梯问题使用的是斐波那契数列列的第2、3项做基本情况。

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
 public class Solution {
    public int climbStairs(int n) {
        int[][] q = {{1, 1}, {1, 0}};
        int[][] res = pow(q, n);
        return res[0][0];
    }
    public int[][] pow(int[][] a, int n) {
        int[][] ret = {{1, 0}, {0, 1}};
        while (n > 0) {
            if ((n & 1) == 1) {
                ret = multiply(ret, a);
            }
            n >>= 1;
            a = multiply(a, a);
        }
        return ret;
    }
    public int[][] multiply(int[][] a, int[][] b) {
        int[][] c = new int[2][2];
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = a[i][0] * b[0][j] + a[i][1] * b[1][j];
            }
        }
        return c;
    }
}

复杂度分析

  • 时间复杂度：$O(\log(n))$。
  • 空间复杂度：$O(1)$。使用固定的空间。

时间复杂度证明：

假设有一个$n$次幂的矩阵$M$，假设$n$是2的幂，那么$n=2^i , i \in \mathbb{N} $，其中$\mathbb {N}$表示自然数集合（包括0）。我们可以用如下形式的树来表示：

图中内容表示：$M^n=M^{n/2}=…=\prod_1^n{M^1}​$。

所以，为了计算矩阵$M^n$，我们需要计算$M^{n/2}$并且和自己相乘。为了计算$M^{n/2}$需要计算$M^{n/4}$，等等等等。

显然，树的高度为$\log_2{n}$。

下面来估计$M^n$的计算时间。矩阵$M$在任意次幂的大小都一样，所以我们可以在$O(1)$的时间内计算任意次幂的两个矩阵相乘。这样的计算需要执行$\log_2{n}$次。所以$M^n$的计算复杂度为$O(\log_2{n})$。

如果$n$不是2的幂，那么我们可以通过其二进制表示将其分解为用2的次幂表示：

这样我们可以通过如下公式来得到最终结果：

这就是在实现中使用的方法？由于乘法的计算次数已经限制在$O(\log_2n)​$，所以总的复杂度就是$O(\log_2n)​$。

方法6、斐波那契公式

没太仔细理解这个方法。。。

我们可以用如下公式计算得到第$n$个斐波那契数：

对于给定的问题，斐波那契数列定义为：$F_0=1,F_1=1,F_2=2,F_{n+2}=F_{n+1}+F_n$。解决这种递归公式的一种标准方法是假设$F_n$的形式为$F_n=a^n$。这样的话，显然$F_{n+1}=a^{n+1}$并且$F_{n+2}=a^{n+2}$，所以等式就变为$a^{n+2}=a^{n+1}+a^n$。如果我们将整个等式除以$a^n$，就得到$a^2=a+1$，也就是二次方程$a^2-a-1=0$。

对这个二次方程求解，可以得到：

对于一般情况，可以得到等式：

对于$n=0$的情况，有$A+B=1$，

对于$n=1$的情况，有$A\left( \cfrac{1+\sqrt 5}{2} \right)+B\left( \cfrac{1-\sqrt 5}{2} \right)=1$，

对上述等式求解，可以得到：

将$A$和$B$的值代入到上述的通用等式中，可以得到：

代码如下：

1
2
3
4
5
6
7
public class Solution {
    public int climbStairs(int n) {
        double sqrt5=Math.sqrt(5);
        double fibn=Math.pow((1+sqrt5)/2,n+1)-Math.pow((1-sqrt5)/2,n+1);
        return (int)(fibn/sqrt5);
    }
}

复杂度分析

  • 时间复杂度：$O(\log(n))$。$pow$计算需要$\log(n)$的时间。
  • 空间复杂度：$O(1)​$。使用固定空间。

四、Complexity Analysis 复杂度分析

在这一章，我们将讨论如何计算递归算法中的时间和空间复杂度。

特别的是，本章将展示一个非常有用的叫做尾递归的技术，可以用来优化递归问题中的空间复杂度，更重要的是可以避免栈溢出的问题。

时间复杂度——递归

这一部分，我们主要讨论如何计算递归问题中的时间复杂度。

给定一个递归问题，其时间复杂度$O(T)$主要是由递归调用的次数（用$R$表示）和每次递归中所需的计算时间（用$O(s)$表示）共同决定的：

来看一些例子。

举例

在反转字符串问题中，我们需要将一个字符串逆序输出。解决这个问题的一个递归关系可以表示如下：

其中$str[1…n]$是输入字符串$str$的子串，$str[0]$是首字符。

可以看到，函数递归调用$n$次，$n$是输入字符串的长度。在每一次递归中，只是简单的输出首字符，所以该操作的时间复杂度是常数级，即$O(1)$。

所以，递归函数$printReverse(str)$的总时间复杂度就是$O(printReverse)=n*O(1)=O(n)$。

执行树

对于递归函数，调用次数刚好和输入成线性关系的情况是很少见的。例如，在上一章讨论过的斐波那契数列问题，递归函数定义为$f(n)=f(n-1)+f(n-2)$。乍一看，斐波那契函数的调用次数并不能够很直观的得到。

在这种情况，最好是采用execution tree 执行树的方式，这种树是用来详细表示递归函数执行过程的。树上的每个节点表示递归函数的一次调用，所以总的节点数就是整个执行过程中递归调用的总次数了。

执行树用一个$n$叉树来表示，其中$n$表示递归关系中出现递归调用的次数。例如，斐波那契数列问题的执行树是一颗二叉树，下图表示了计算斐波那契数$f(4)$的执行树：

对于一个$n$层的二叉树，其节点总数是$2^n-1$。所以，$f(n)$递归调用次数的上限（虽然不是很严格）就是$2^n-1$。所以，可以得到斐波那契数列问题$f(n)$的时间复杂度是$O(2^n)$。

缓存计算

在上一章，讨论过递归算法中用于优化时间复杂度的方法——缓存计算。通过将中间结果进行缓存和重复使用，缓存计算可以大幅减少递归调用的次数，也就是减少执行树的分支数。所以应该考虑到使用缓存计算的递归算法时间复杂度。

回到斐波那契数列问题，使用缓存计算的话，可以将每个斐波那契数的结果进行保存。保证对每个斐波那契数的计算只执行一次。由递归关系可以知道，对于斐波那契数$f(n)$，依赖于前$n-1$个斐波那契数，所以，$f(n)$的递归计算过程将会调用$n-1$次，来计算其所依赖的所以前序数值。

现在可以直接使用本章开始时候给出的公式来计算时间复杂度，即$O(1)*n=O(n)$。缓存计算不仅优化了算法的时间复杂度，也简化了时间复杂度的分析过程。

接下来，我们讨论如何分析递归算法的空间复杂度。

空间复杂度——递归

这一部分，将讨论如何分析递归算法中的空间复杂度。

当讨论递归算法的空间复杂度时，应该考虑两部分的空间消耗：递归相关的空间和非递归相关的空间。

递归相关的空间

递归相关的空间指的是由递归调用所直接产生内存消耗，即保存递归函数调用所需的栈空间。为了完成一个典型的递归调用，系统需要分配一些空间来保存三部分重要的信息：

  1. 函数的返回地址：一旦函数调用完成，程序应该知道返回到哪里，即函数调用之前的位置；
  2. 函数传递的参数；
  3. 函数的局部变量；

这个栈空间是函数调用过程中所产生的最小开销，一旦函数执行结束，空间就会被释放。

对于递归算法，函数调用会链式累积，直到到达基本情况。这意味着每个函数调用所需的空间也会累积。

对于递归算法，如果没有其他内存消耗，那么这个由递归行为本身所引起的空间消耗将会是整个算法的空间上限。

例如，在逆序输出字符串的练习中，由于只是单纯的输出字符，所以在递归调用本身之外没有额外的空间消耗。对于每一个递归调用，我们假设需要一个常数级的空间。递归调用将持续$n$次，$n$是输入字符串的长度。所以这个递归算法的空间复杂度是$O(n)$。

为了说明这一点，以递归调用$f(x_1)\rightarrow f(x_2)\rightarrow f(x_3)$为例，展示了执行步骤的顺序和堆栈布局。

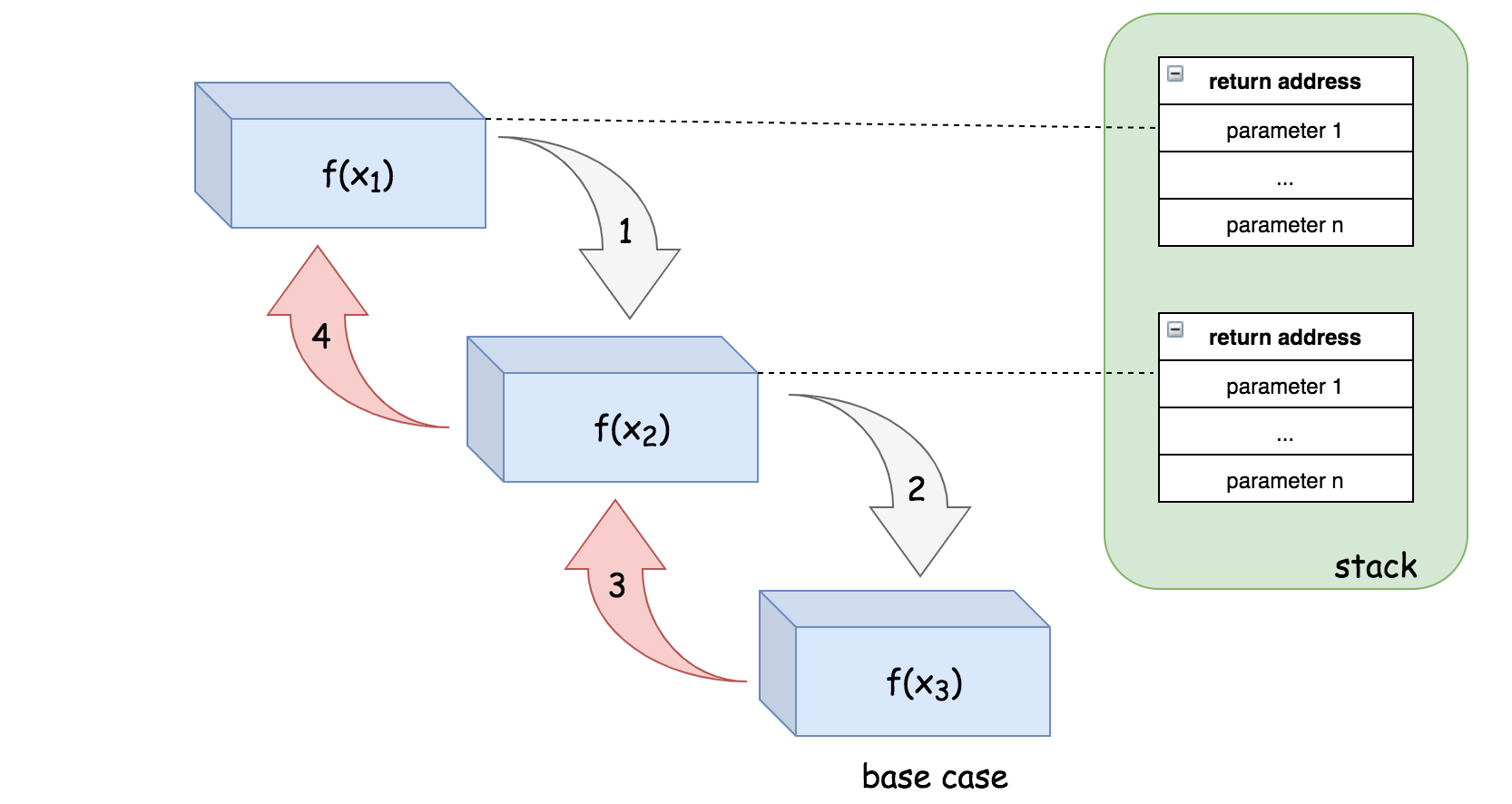
为了调用$f(x_2)$，会给$f(x_1)$分配一个栈空间。同理，在$f(x_2)$中也会为了调用$f(x_3)$而分配另一个栈空间。最终在$f(x_3)$中，程序到达基本情况，因此没有在$f(x_3)$中进一步递归。

由于这些递归相关的空间消耗，有时会导致栈溢出的情况，就是分配给一个程序的栈空间超出了其最大空间限制，导致程序失败。因此，当设计递归算法时，要仔细考虑当输入规模比较大的时候是否可能导致栈溢出。

非递归相关的空间

如标题所示，非递归相关的空间主要是指和递归没有直接关系的内存空间，通常包括分配给全局变量的空间（通常为堆）。

不论是否递归，在任何后续函数调用前都需要将问题的输入作为全局变量保存。同时还需要存储递归调用的中间结果。后者就是我们在前面章节讨论过缓存计算。例如，对于使用缓存计算实现的计算斐波那契数列的递归算法，我们使用一个map来记录递归调用过程中出现的所有斐波那契数。因此，在分析空间复杂度的时候，我们应该考虑到缓存计算的空间成本。

尾递归

在之前的页面，讨论过递归调用过程中系统分配栈空间所产生的隐藏空间开销。但是，我们应该学会识别一种递归的特殊情况——尾递归，尾递归避免了这部分空间开销。

尾递归是指在递归函数执行的最后命令是递归调用，并且应该只有一个递归调用。

在反转字符串的问题中我们已经看到了一个尾递归的例子。这里用另一个例子展示非尾递归和尾递归的区别。注意，非尾递归的例子在最后一个递归调用之后有一个额外的计算步骤。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def sum_non_tail_recursion(ls):
    """
    :type ls: List[int]
    :rtype: int, the sum of the input list.
    """
    if len(ls) == 0:
        return 0
    
    # not a tail recursion because it does some computation after the recursive call returned.
    return ls[0] + sum_non_tail_recursion(ls[1:])


def sum_tail_recursion(ls):
    """
    :type ls: List[int]
    :rtype: int, the sum of the input list.
    """
    def helper(ls, acc):
        if len(ls) == 0:
            return acc
        # this is a tail recursion because the final instruction is a recursive call.
        return helper(ls[1:], ls[0] + acc)
    
    return helper(ls, 0)

尾递归的好处是可以避免递归调用过程中的堆栈开销累积，因为系统在每次递归调用的时候可以重复利用一部分栈空间。

以递归调用$f(x_1)\rightarrow f(x_2)\rightarrow f(x_3)$为例，其中函数$f(x)$是使用尾递归实现的，如下展示了执行步骤的顺序和堆栈布局。

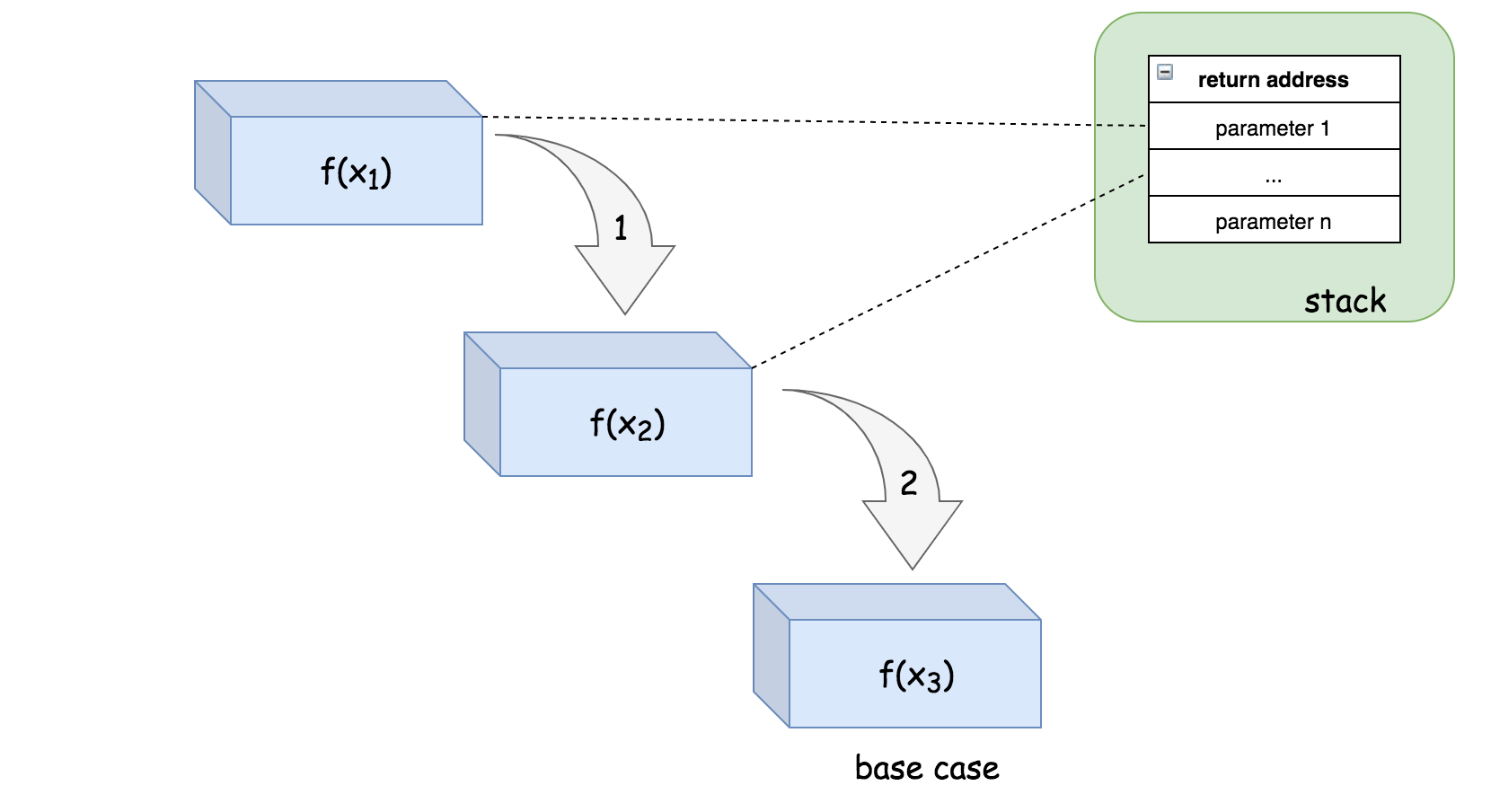
注意在尾递归中，一旦递归调用结束，我们就会理解知道返回值，所以图中跳过了递归返回的完整链路，直接返回到原始调用的地方。这意味着，我们不再需要对所有递归调用都分配栈，从而节省了空间。

例如，在步骤1中，为了调用$f(x_2)$而在$f(x_1)$中分配了栈空间。在步骤2中，$f(x_2)$会递归调用$f(x_3)$，但是系统可以直接重复使用之前为第二次递归调用分配的空间，而不是分配新的空间。最终，在函数$f(x_3)$中，我们到达了基本情况，函数可以直接返回到原始调用的地方，而不需要逐步返回到上一个调用的函数。

尾递归函数可以当做非尾递归函数执行，也就是调用成堆的栈，而不影响结果。通常，编译器会识别尾递归并优化执行过程。但是，并不是所有语言都支持这种优化。例如，C、C++支持尾递归优化，而Java和Python不支持尾递归优化。

练习：二叉树的最大深度

详见【LeetCode】104、二叉树的最大深度

Given a binary tree, find its maximum depth.

The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Note: A leaf is a node with no children.

Example:

Given binary tree [3,9,20,null,null,15,7],

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

return its depth = 3.

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if (root==NULL)
            return 0;
        if (root->left==NULL && root->right==NULL)
            return 1;
        
        int leftDepth = maxDepth(root->left);
        int rightDepth = maxDepth(root->right);
        if (leftDepth > rightDepth) {
            return leftDepth+1;
        }
        else {
            return rightDepth+1;
        }
    }
};

解答：二叉树的最大深度

要花钱才能解锁，没有看:joy:。

练习：Pow(x, n)

详见【LeetCode】50、Pow(x,n)

Implement pow(x, n), which calculates x raised to the power n (xn).

Example 1:

1
2
Input: 2.00000, 10
Output: 1024.00000

Example 2:

1
2
Input: 2.10000, 3
Output: 9.26100

Example 3:

1
2
3
Input: 2.00000, -2
Output: 0.25000
Explanation: 2-2 = 1/22 = 1/4 = 0.25

Note:

  • -100.0 < x < 100.0
  • n is a 32-bit signed integer, within the range $[-2^{31},2^{31}-1]​$

代码如下：

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    double myPow(double x, int n) {
        if (n == 0) return 1;
        double half = myPow(x, n / 2);
        if (n % 2 == 0) return half * half;
        if (n > 0) return half * half * x;
        return half * half / x;
    }
};

解答：Pow(x, n)

要花钱才能解锁，没有看:joy:。

五、Conclusion 总结

在之前的章节，我们了解了递归的概念的原则。

作为提醒，以下是解决递归问题的共用工作流程：

  1. 定义递归函数；
  2. 总结递归关系和基本情况；
  3. 如果有重复计算问题的话，使用缓存计算来消除；
  4. 如果可能，使用尾递归来优化空间复杂度；

在本章，将对递归算法做一些总结，并且提供一些在利用递归解决问题的过程中可能用到的tips。

总结——递归-1

现在，我们了解到递归确实是一个可以用来解决很多问题的有效方法。但是，由于时间和空间的限制，并不是所有问题都能用递归解决。递归可能会有一些负面效果，如栈溢出问题。

在这章，将分享一些可以更好的利用递归来解决实际问题的tips：

疑惑的时候，把递归关系写下来。

有时，乍一看，问题能够用递归算法解决并不明显。但是，由于递归算法和我们所熟悉的数学非常接近，所以利用数学公式推导出一些关系式总是有帮助的。通常，可以帮助澄清问题概念并揭示隐藏的递归关系。在本章后面，可以通过一个例子（Unique Binary Search Trees II）来了解在数学公式的辅助下利用递归方法解决问题。

如果可能，使用缓存计算。

在起草递归算法的时候，可以从最简单的策略开始。有时，在递归过程中会存在重复计算，如斐波那契数问题。在这种情况下，应该尝试使用缓存计算技术，将中间结果缓存以后后续重复使用。缓存计算利用空间上的一些折中来换取时间复杂度的大幅提升。

当出现栈溢出问题时，尾递归可能会有帮助。

使用递归算法通常有几种不同的实现。尾递归是其中一个特定的实现形式。和缓存计算不同，尾递归可以通过消除递归算法带来的堆栈开销来优化算法的空间复杂度。更重要的是，使用尾递归可以避免递归算法常出现的栈溢出问题。尾递归的另一个优点是比非尾递归更容易阅读和理解。因为和非尾递归不同，尾递归中不存在递归后调用的问题（即递归操作是函数的最后操作）。所以，只要可能，应该尽量使用尾递归。

后续

现在，利用目前为止所了解到的递归知识，可以在LeetCode上解决更多问题。在本章中，还提供了几个练习。

练习：合并两个有序链表

详见【LeetCode】21、合并两个有序链表

Merge two sorted linked lists and return it as a new list. The new list should be made by splicing together the nodes of the first two lists.

Example:

1
2
Input: 1->2->4, 1->3->4
Output: 1->1->2->3->4->4

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        if (l1==NULL)
            return l2;
        if (l2==NULL)
            return l1;
        if (l1->val<l2->val) {
            l1->next = mergeTwoLists(l1->next, l2);
            return l1;
        }
        else {
            l2->next = mergeTwoLists(l1, l2->next);
            return l2;
        }
    }
};

解答：合并两个有序链表

要花钱才能解锁，没有看:joy:。

练习：第k个语法符号

详见【LeetCode】779、第k个语法符号

On the first row, we write a 0. Now in every subsequent row, we look at the previous row and replace each occurrence of 0with 01, and each occurrence of 1 with 10.

Given row N and index K, return the K-th indexed symbol in row N. (The values of K are 1-indexed.) (1 indexed).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Examples:
Input: N = 1, K = 1
Output: 0

Input: N = 2, K = 1
Output: 0

Input: N = 2, K = 2
Output: 1

Input: N = 4, K = 5
Output: 1

Explanation:
row 1: 0
row 2: 01
row 3: 0110
row 4: 01101001

Note:

  1. N will be an integer in the range [1, 30].
  2. K will be an integer in the range [1, 2^(N-1)].

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int kthGrammar(int N, int K) {
        if (N==0)
            return 0;
        if (K%2 == 0) {
            return kthGrammar(N-1, K/2)==0 ? 1:0;
        }
        else {
            return kthGrammar(N-1, (K+1)/2)==0 ? 0:1;
        }
    }
};

解答：第k个语法符号

要花钱才能解锁，没有看:joy:。

练习：不同的二叉搜索树II

Given an integer n, generate all structurally unique BST’s (binary search trees) that store values 1 … n.

Example:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Input: 3
Output:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST's shown below:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

等复习了二叉树再后续补充，，，

解答：不同的二叉搜索树II

要花钱才能解锁，没有看:joy:。

-------------本文结束感谢您的阅读-------------
0%